Experiments are hard work and can be difficult to design and analyze. The University of Minnesota conducts many agronomic experiments, as do other public institutions and agricultural companies.
Even with this abundance of information, you may want to conduct your own on-farm experiment/trial. For example, you may:
-
Want to test agronomic practices or products that you can’t find adequate information about.
-
Have a unique condition on your farm that you think would produce atypical results.
-
Have a healthy skepticism and need to see things for yourself. For example, you might want to compare yields of corn hybrids, a foliar fungicide compared to not treating or how two tillage systems affect soybean yield.
Below, we provide some advice for planning and analyzing your experiments.
Conducting your own on-farm experiments
Take care when selecting field areas where you’ll place the blocks or strips of your trial treatments (things you’re trying to compare). As much as possible, avoid areas of the field with obviously different drainage, topography/soil type and recent cropping histories.
Try to select areas similar in yield potential and any other effect you’re trying to test with your treatments—for example, crop pests. In the soybean yield map shown in Figure 1, notice the variable yield due to soil conditions. If treatments were placed in this field as the red boxes indicate, yield differences because of field conditions are likely to overwhelm any treatment comparisons.
Additionally, individual fields can vary greatly in cropping and management histories. It’s risky to compare two fields—for example, one treated with insecticide and one untreated—and draw an accurate conclusion on the treatment’s effectiveness.
Except for what you’re trying to compare, keep as many things as possible the same. Use the same seed lot, planting date, equipment and non-tested additives for all treatments.
When variables other than the one you’re testing influence comparisons, the data are said to be confounded. It’s difficult, if not impossible, to determine the real treatment effects in your trial if there were confounding factors affecting the results.
Examples: Situations that can confound results
For example, if you’re running a ground sprayer as part of your experiment, run the sprayer with the booms off in the untreated treatment areas. This will keep things fair in case you harvest any wheel track areas in your sprayed areas.
Comparing a treatment containing nitrogen fertilizer with one that doesn’t may confound your results if the fertilizer affects crop growth. Yield differences when comparing treated and untreated seed from different seed lots might be due to the seed treatment or to the seed itself.
Whether you’re measuring the weights of a group of people or crop yields in a field, few, if any, measurements are exactly the same. The previous yield map example shows that if you take multiple yield measurements, you’re likely to end up with multiple yield estimates for the field.
The more measurements or samples you take, the more likely you’ll closely estimate the field’s actual yield. If you take enough samples, you’ll know the field’s average (or mean) yield and how variable the yield within the field is.
Diagramming the distribution
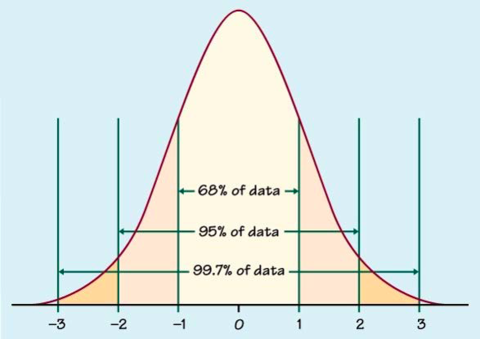
You could take the field’s yield and diagram it similarly to the normal distribution graph (the bell-shaped curve shown in Figure 2). You’d have approximately the same number of sampled yields that are above the mean as sampled yields that are below.
When you’re comparing experimental results for two or more treatments, you’re comparing the means of the treatments. The variability of those two means determines how easy it is to make those comparisons and detect differences.
When the data don’t follow this symmetrical, normal relationship, correct analysis is more difficult. Fortunately, yields typically are normally distributed.
When you set up an experiment in a field, you’re only obtaining yield estimates from part of the field.
If you compare a single strip with fungicide to a strip without, you have two yield samples, but no estimate of how variable the measurements are within the field and within treatment. In statistical terms, you have a single replication of each treatment.
What happens if you don’t take enough samples
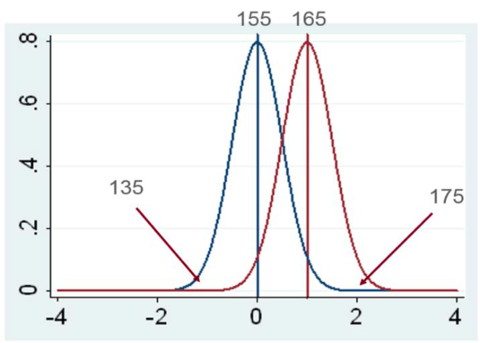
Depending on how and where you took the samples, they could be representative of the results or they could be on one of the curve’s tails (as shown in Figure 3).
For example, in Figure 3, is the difference between treatments 40 or 10 bushels? Depending on which samples you take, a trial’s treatment differences will appear larger than they actually are or you’ll find differences that aren’t real.
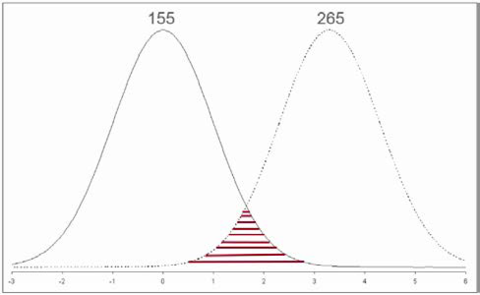
On the other hand, your single samples may both represent an area where the tails of the two treatments overlap, indicating yields are the same (Figure 4). How would you know?
Replicating treatments
Taking more samples within a treatment area will give you an estimate of variability within that treatment. However, simply taking more samples within a treatment won’t improve your ability to measure variability across the field.
Repeating treatments by replicating plots or strips enables you to assess the variability and estimate the mean across the field. More replications will improve your ability to accurately estimate means, variability and differences between treatments.
Aim to replicate each treatment at least three times. Space constraints will limit the number of treatment replications possible with farm-scale equipment.
Because of within-field variability and inconvenient statistical analysis assumptions on randomness and equal probabilities, you need to pay some attention to how you place treatment replications in the field.
Obviously, placing all replications for one treatment at one end of the field and all replications of the other treatment at the other end could lead to erroneous conclusions. It could even mean you have multiple samples for a single replication of each treatment.
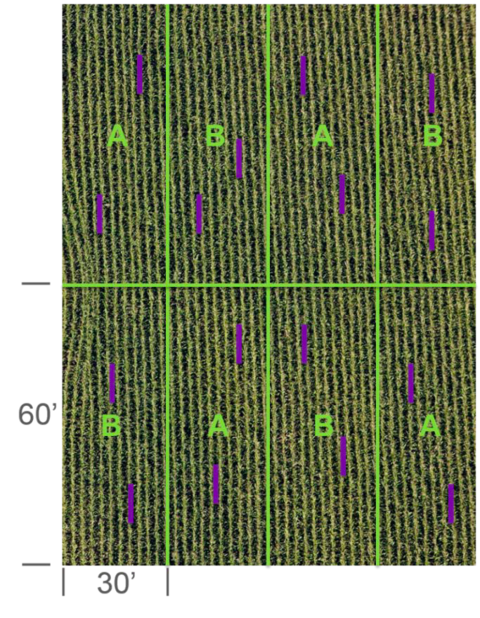
Avoid regularly alternating the plots when possible. This is because soil type and other variability within the field aren’t regularly or uniformly placed. Regular alternation might be unavoidable with only a couple treatments in a field (Figure 5). You can randomize where you place plots or strips with a calculator function or a even a coin flip.
Multiple samples within a plot or a strip are known as subsamples; they’re not replicates. Subsamples can improve the accuracy estimates of a plot, but not between plots.
Avoid analyzing these subsamples as individual plot means or replicates. This is known as pseudo replication.
Interpreting your experiment’s results
Just like deciding on and placing your treatments, how you interpret the results can make a big difference in the conclusions’ usefulness.
Here, we’ll assume we’re comparing yield between two or three treatments and that yields follow the normal distribution (the bell-shaped curve). The curve’s shape will determine how easy it’ll be to draw good conclusions from your data.
If the data’s distribution has narrow tails, most samples you take will be close to the true mean. If the data are more variable because of inconsistent responses to your treatment or uncontrollable variables such as soil type, the curve’s tails will spread out farther from the true mean.
If you conduct a field experiment comparing, for example, corn yield from multiple treatments, you only have yield from the replications. This is only a subset of data representing the possible yield in the field (or other fields) for each treatment—you don’t know the true mean of each treatment. In other words, you’re comparing sample means to estimate the true means.
It’s easier to accurately estimate true treatment means for data that’s less variable. You’re less likely to obtain a similar treatment mean when you take additional samples for an experiment that has highly variable data.
Highly variable data lacks precision and can lead to much different, less accurate mean estimates if you resample or repeat the experiment. Taking more samples (replications) is one way to improve accuracy.
It’s easy to estimate the treatment means for your experiment—you simply average the replicated samples for each treatment. You can estimate variability by calculating the standard deviation of the mean.
Standard error of the mean (SEM) calculations include the number of replicated samples in your mean:
SEM = Standard deviation ÷ (√number of samples - 1)
A simple way to compare two treatments is to compare the two means as mean plus or minus standard error. If means differ by more than 1 standard error, the true means are probably different. If they differ by 2 SEM, they’re even more likely to be different.
You can calculate confidence intervals to describe how confident you can be in the accuracy of:
-
Your mean estimation.
-
Comparisons between means.
A 90 percent confidence interval (C.I.) means there’s a 90 percent probability that the true mean lies within your range of estimated values. When thinking about C.I., remember the normal distribution curve. The 90 percent C.I. means 45 percent of the possible sample results would be greater than the average and 45 percent below.
It also means there’s a 10 percent chance your results are outside those limits (5 percent above and 5 percent below). This 10 percent chance is usually referred to as alpha or α. Least significant difference (LSD) values of .10 or 10 percent are similar.
Standard confidence interval
Other alpha values and C.I. probabilities can be calculated, with 80 percent being used in some variety testing evaluations. Academic research commonly uses 95 percent as a standard, although sometimes the requirement is 99 percent or even 99.9999 percent, when NASA wants to land a rover on Mars.
Errors of various confidence intervals
As exemplified in Figure 6, selecting 80 or 95 percent would indicate the means being compared are different. Selecting the very strict 99 percent would indicate they’re not.
Unless we sampled all treatment combinations in all fields, we don’t know what the true mean is. It’s your decision as to which type of error you’re more willing to risk: Saying the means are different when they’re not (Type I error) or saying means are the same when they’re different (Type II error).
How to select a confidence interval
Choosing a low C.I., like 80 percent, means you’re more likely to find different means but are less confident that they’re actually different. Choosing a high C.I., like 90 percent, increases the probability that you’re making the correct decision on whether the two means are different but also increases the chance you’ll miss real treatment differences.
Lower confidence interval situations
If you’re choosing between treatments that have little downside you could use a lower confidence interval for your test. For example:
-
Whether an insecticide provides a yield benefit in your field.
-
Which hybrid yielded more.
Higher confidence interval situations
If there’s a significant economic, safety or health risk, use a higher confidence interval. The following would benefit from interpreting comparisons with a higher degree of confidence (e.g., 95 percent or more) and testing under more environmental conditions:
-
Statewide pesticide recommendations.
-
Comparing the stability of explosive formulations.
-
Pharmaceutical safety testing.
Spreadsheet for making comparisons
We’ve prepared an Excel spreadsheet for comparing two or three treatments using a two-tailed t-test. With the spreadsheet, you can:
-
Select the precision (80, 90 or 95 percent confidence interval) for your comparison and enter three to eight replicated samples for each treatment. Use real replicates, not the pseudo replicates mentioned earlier.
-
Experiment with different replicate sample averages and variabilities, replicate numbers and confidence intervals.
-
Compare yield, plant populations, percent control for crop protection chemicals and other treatments.
Tips for on-farm research
-
Don’t try to compare too many treatments in one trial. If you’re trying to compare more than three or four treatments, seek help from a statistician.
-
Make sure you have a control treatment. Include a common treatment or untreated plots in your comparison.
-
Avoid placing treatments in locations that would affect treatments differently—for example, consider cropping history and soil factors.
-
Include replications. You need three or more replicates (plots for each treatment) to determine the consistency of results. Multiple samples from the same plot or strip isn’t replication; those are pseudo replications.
-
Randomize the order of your treatment plots or strips in the field. This refers to the planting order of varieties, or which plots receive which varieties.
-
Understand how variability influences your ability to draw conclusions. Do you want to risk calling treatments different when they’re essentially the same? Or do you want to risk not finding real treatment differences?
-
Don’t over-extrapolate and assume the rest of your experiment has to be valid for other fields.
Reviewed in 2022